close;clc;clear
A=[0 0 0];
B=[0 1 0];
C=[0 1.9 0.3];
D=[0.2 2.8 0.9];
%% 1 首先求得辅助的各个单位法向量
E=cross(B-A,C-A);%AB AC叉乘
E=E./norm(E); %单位法向量
F=cross(C-D,B-D); %DC DB叉乘
F=F./norm(F)+D;
F0=F-D;%单位法向量,注意,作用在D点要+D
m1=cross(F0,E); %两个面的法向量叉乘
m1=m1./norm(m1); %单位化
m2=C-B; %向量BC
m2=m2./norm(m2); %单位化
%% 2 用n1,n2(两个面的法向量)求两个相邻面夹角(用°表示角度)
n1=-F0; n2=E;
cetan=(acos(sum(n1.*n2)/(0.0001+sum(n1.^2)^0.5*sum(n2.^2)^0.5)))/pi*180
%% 3 区分两个面的夹角方向
%1/求两个面法向量叉乘结果与BC的夹角(用°表示角度),进而获得sign
ceta=(acos(sum(m1.*m2)/(0.0001+sum(m1.^2)^0.5*sum(m2.^2)^0.5)))/pi*180;
if ceta>=90,sign=-1,ceta, end %如果夹角为顿角, sign=-1
if ceta<90, sign=1, ceta, end %如果夹角为锐角, sign=1
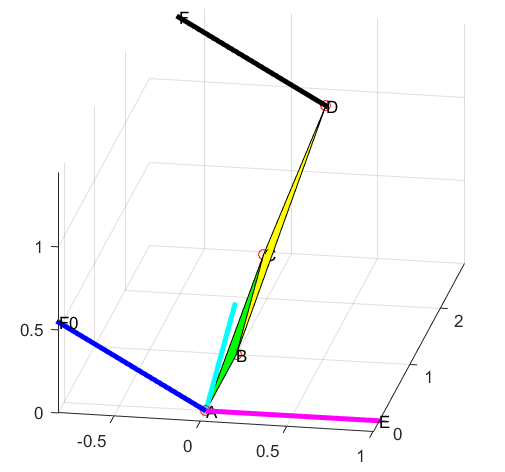
%% 以下为图像的辅助显示------------------------------------------
hold on
line([A(1),B(1)],[A(2),B(2)],[A(3),B(3)],'color','r');
line([B(1),C(1)],[B(2),C(2)],[B(3),C(3)],'color','r');
line([C(1),A(1)],[C(2),A(2)],[C(3),A(3)],'color','r');
line([C(1),D(1)],[C(2),D(2)],[C(3),D(3)],'color','b');
line([B(1),D(1)],[B(2),D(2)],[B(3),D(3)],'color','b');
fill3([A(1),B(1),C(1)],[A(2),B(2),C(2)],[A(3),B(3),C(3)],'g');
fill3([B(1),C(1),D(1)],[B(2),C(2),D(2)],[B(3),C(3),D(3)],'y');
line([A(1),E(1)],[A(2),E(2)],[A(3),E(3)],'color','m','linewidth',3);
line([A(1),F0(1)],[A(2),F0(2)],[A(3),F0(3)],'color','b','linewidth',3);
line([A(1),m1(1)],[A(2),m1(2)],[A(3),m1(3)],'color','c','linewidth',3);
line([D(1),F(1)],[D(2),F(2)],[D(3),F(3)],'color','k','linewidth',3);
text(A(1),A(2),A(3),'A');
text(B(1),B(2),B(3),'B');
text(C(1),C(2),C(3),'C');
text(D(1),D(2),D(3),'D');
text(E(1),E(2),E(3),'E');
text(F(1),F(2),F(3),'F');
text(F0(1),F0(2),F0(3),'F0');
plot3(A(1),A(2),A(3),'ro');
plot3(B(1),B(2),B(3),'ro');
plot3(C(1),C(2),C(3),'ro');
plot3(D(1),D(2),D(3),'ro');
hold off;
view(10,15);
axis equal;
grid on;

